Note: All comments and opinions expressed on "MATLAB for everyone" are mine alone and do not necessarily reflect those of my employers, past or present.

벡터란 무엇일까?

MATLAB에서 벡터¹란 numeric 타입 변수의 일종이다. 아래의 그림을 보면 다양한 numeric 타입들 간의 포함 관계를 확인할 수 있다.

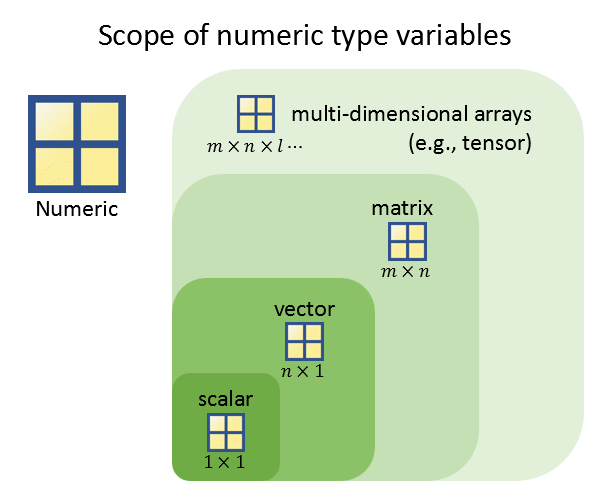
위 그림에서 볼 수 있는 것 처럼 스칼라가 숫자 하나를 나타낸 것이라면 벡터는 여러개 숫자를 일렬로 나열한 것이다. 예를 들면, 아래는 스칼라 하나와 세 개의 숫자로 구성된 벡터를 나타낸 것이다.

\[\text{scalar: } 3\text{, vector: } \begin{bmatrix} 3 \\ 2 \\ 5 \end{bmatrix}\]

보통 n 개의 숫자로 구성된 벡터를 “n 차원 벡터(n-dimension vector)”라고 부른다. “차원”이라는 말이 붙은 것은 2 차원 혹은 3 차원 공간의 한 점이 각각 두 개의 숫자 나열 혹은 세 개의 숫자 나열로 표현될 수 있기 때문에 이 개념이 확장된 것이다. 4 차원 이상의 벡터는 시각적으로 공간 상의 점으로 나타낼 수는 없지만 숫자의 나열을 모아둔 것이라는 의미를 지니게 된다. 아래의 그림 처럼 숫자를 일렬로 네 개 나열한 것이 4차원 벡터이다. “4차원”이라는 이름만 복잡할 뿐 전혀 어려운 개념이 아니다.

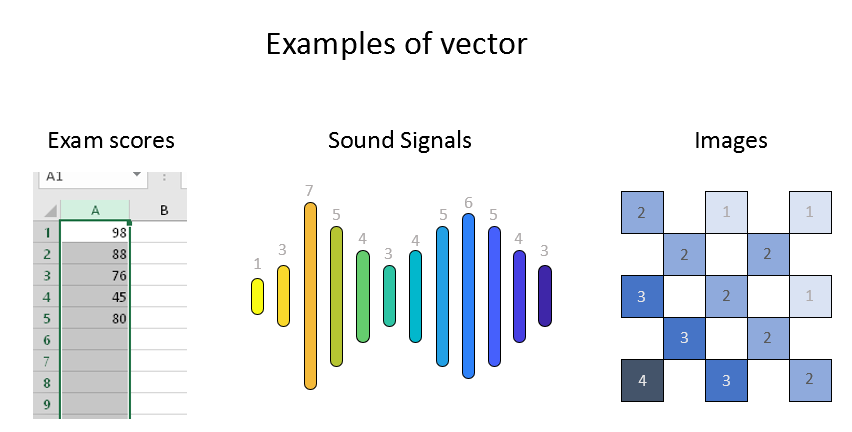
그렇다면 벡터를 왜 배워야 할까? 다르게 말하면 벡터를 배워서 어떻게 쓸 수 있을까? 벡터가 유용한 이유는 우리가 다루는 모든 데이터를 “벡터”의 단위로 쪼개 생각할 수 있기 때문이다. 다시 말해, 모든 데이터들을 “숫자의 나열”로 생각해볼 수 있다는 의미이다. 가령, 성적표는 숫자의 나열로 생각할 수 있다. 국어, 영어, 수학, 과학, 사회 성적을 순서대로 나열할 수 있다. 또, 음성 신호는 긴 숫자의 나열이다. 시간 순서에 따른 신호의 높낮이를 숫자로 표현할 수 있기 때문이다. 또, 이미지도 숫자들의 나열이다. 2차원의 형태로 픽셀의 밝기를 숫자로 표현할 수 있기 때문이다.

벡터를 이용하는 함수

MATLAB에서는 수 많은 함수들이 벡터를 입력 받거나 출력해준다. 벡터를 입/출력하는 가장 간단한 함수는 덧셈이라고 할 수 있다. 덧셈이 왜 함수냐라고 생각할 수 있겠지만, 함수는 간단하게 말해 입력과 출력 간의 관계를 표현해주는 것이기 때문에 덧셈 연산은 두 개의 입력을 받고 하나의 출력을 내보내는 함수라고도 말할 수 있는 것이다.

덧셈 연산자는 아래와 같이 벡터 연산을 수행할 수 있다.

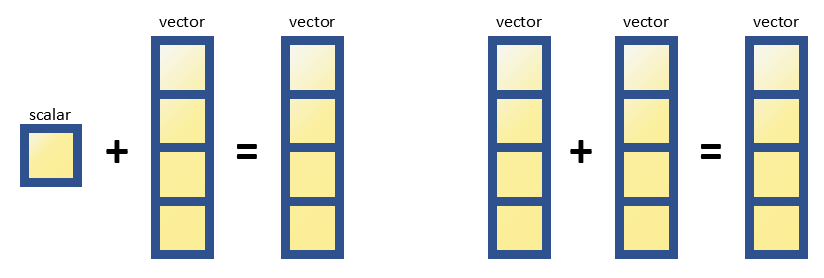
또 다른 예시는 사인(sine) 함수가 있을 수 있겠다. 사인 함수는 벡터를 입력으로 받고 벡터를 출력해준다.

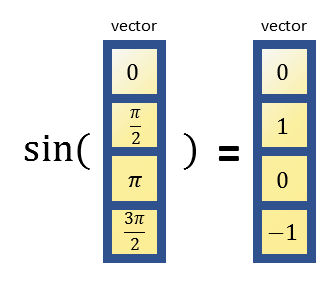
벡터를 입력으로 받고 스칼라를 출력해주는 함수도 있을 수 있다. 가령 sum 함수는 모든 벡터 원소들을 더해준 값을 스칼라로 출력해줄 수 있다.

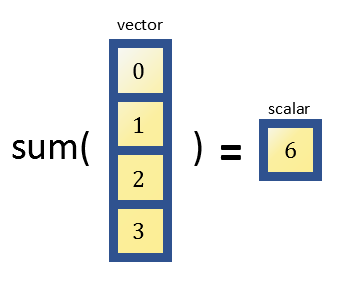
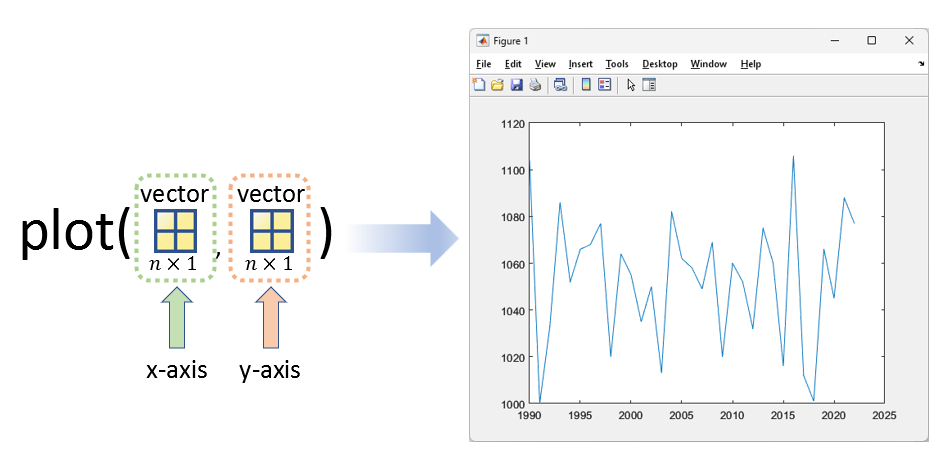
추가로, 어떤 함수들은 두 개 이상의 벡터나 스칼라를 입/출력해줄 수 있다. 가령, 이전 시간에 배운 “plot” 함수는 벡터 두 개를 입력으로 받을 수 있다. 이전 시간에 “my_matfile.mat” 안에 들어있는 “year1”과 “price1”을 plot했던 과정을 다시 한번 생각해보자.

my_matfile.mat 받기

plot(year1, price1);

plot 함수에 들어가는 첫번째 벡터는 x 축에 사용될 정보를 담고 있고, 두 번째 벡터는 y 축에 사용될 정보를 담고 있다. plot 함수는 벡터를 출력하지는 않고 figure를 띄워주고 거기에 그래프를 그려주는 기능을 한다.

이외에도 수많은 MATLAB의 내장함수들이 벡터를 입력으로 받아 내부 데이터들을 일괄 처리해주어서 벡터로 출력해준다. 가령, “exp”, “abs”, “sqrt”, “max”, “min”, “sum”, “mean” 등이 있을 수 있겠다. 이러한 작동은 MATLAB 언어가 벡터 연산에 특화된 고수준 언어라는 점이 부각되는 부분이다. C, Java 등의 상대적으로 저수준의 언어에서는 배열을 포함한 연산을 수행하기 위해선 번거로운 점이 많다.

벡터를 직접 정의하기

대괄호(“[ ]”)를 이용한 벡터, 행렬 정의

선형대수학에서는 아래와 같이 벡터, 행렬을 대괄호에 적기도 한다.

\[A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\]

이 점에 착안한 것인지 MATLAB은 대괄호 사이에 숫자를 집어 넣어 벡터 및 행렬을 정의할 수 있다.

우선, 행벡터(row vector)를 정의해보자. 행벡터는 아래와 같이 양 옆으로 숫자를 나열한 것이다.

\[r = \begin{bmatrix}1 & 2 & 3 \end{bmatrix}\]

MATLAB Command Window에 아래와 같이 입력해보자.

r = [1, 2, 3]

아래와 같이 “r” 이라는 변수가 정의되는 것을 알 수 있으며, Workspace에 있는 “r”을 더블클릭해보면 스프레드시트 같은 곳에 1, 2, 3이 한 줄로 적힌 것을 볼 수 있다.

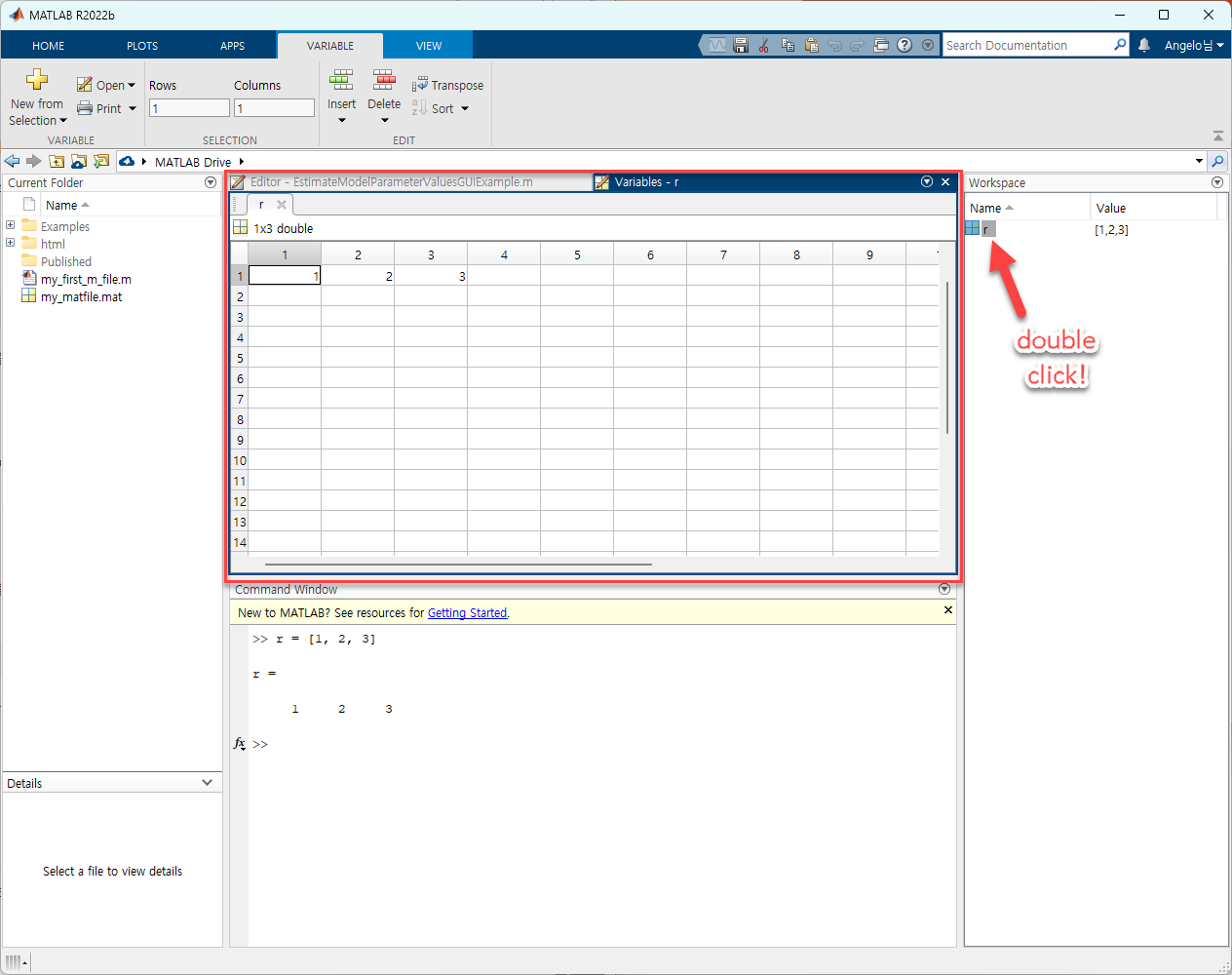
이번엔 열 벡터(column vector)를 정의해보자. 열벡터는 아래와 같이 위 아래로 숫자를 나열한 리스트인데,

\[c = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\]

MATLAB에서는 한 칸 밑으로 내려 적는 것을 세미콜론을 이용해 표시할 수 있다. MATLAB Command Window에 아래와 같이 입력해보자.

c = [1; 2; 3]

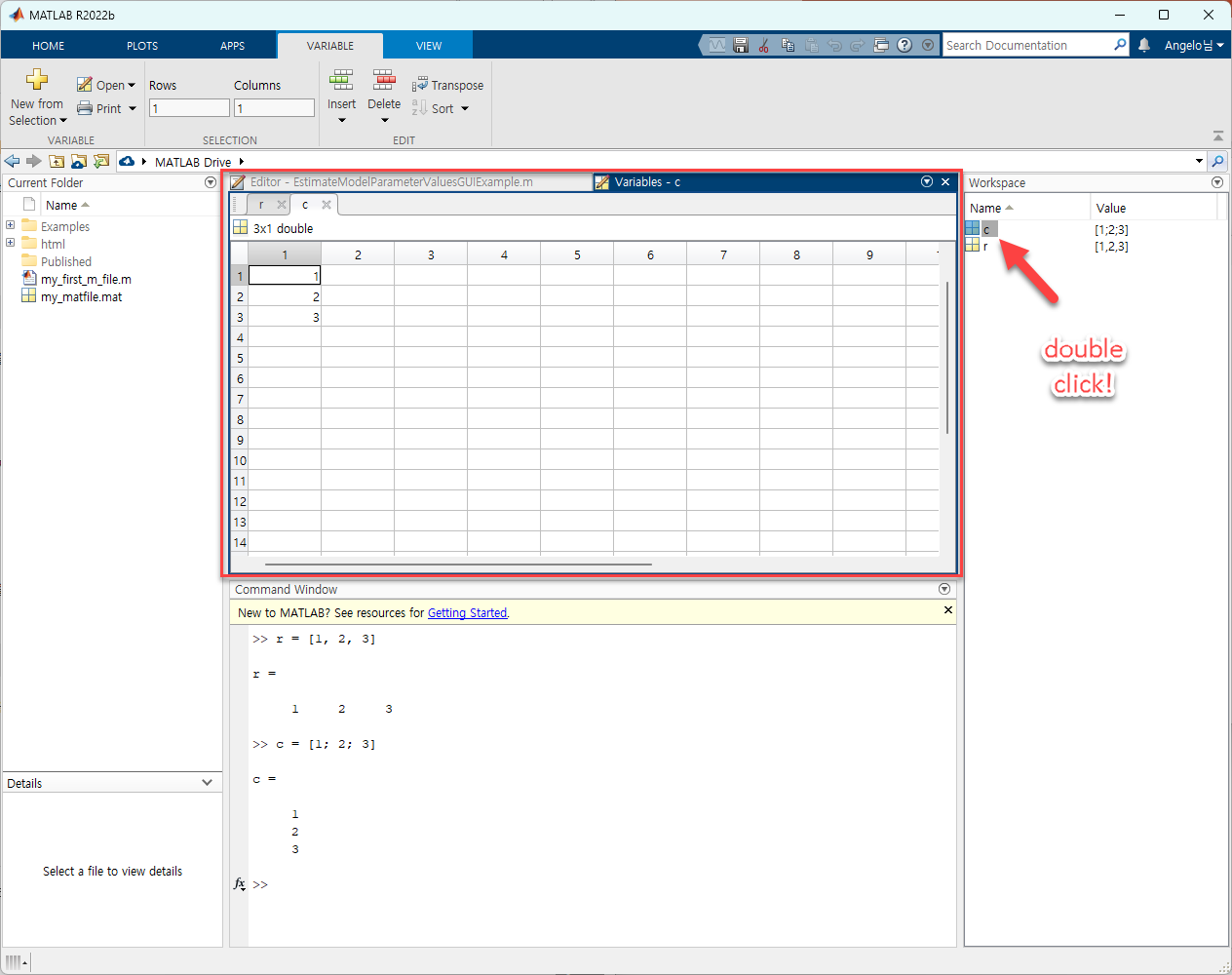
아래와 같이 “c” 이라는 변수가 정의되는 것을 알 수 있으며, Workspace에 있는 “c”를 더블클릭해보면 스프레드시트 같은 곳에 1, 2, 3이 세로로 적힌 것을 볼 수 있다.

등간격 벡터 만들기

아래와 같은 벡터를 생성해야 할 필요가 있는 경우를 상정해보자.

\[x = \begin{bmatrix}1 & 2 & 3 & 4 & 5 & \cdots & 100\end{bmatrix}\]

MATLAB에서는 이런 경우를 생각해 등간격 벡터 생성 방법을 마련해두었다.

Command Window에 아래와 같이 입력해보자.

x = 1:1:100;

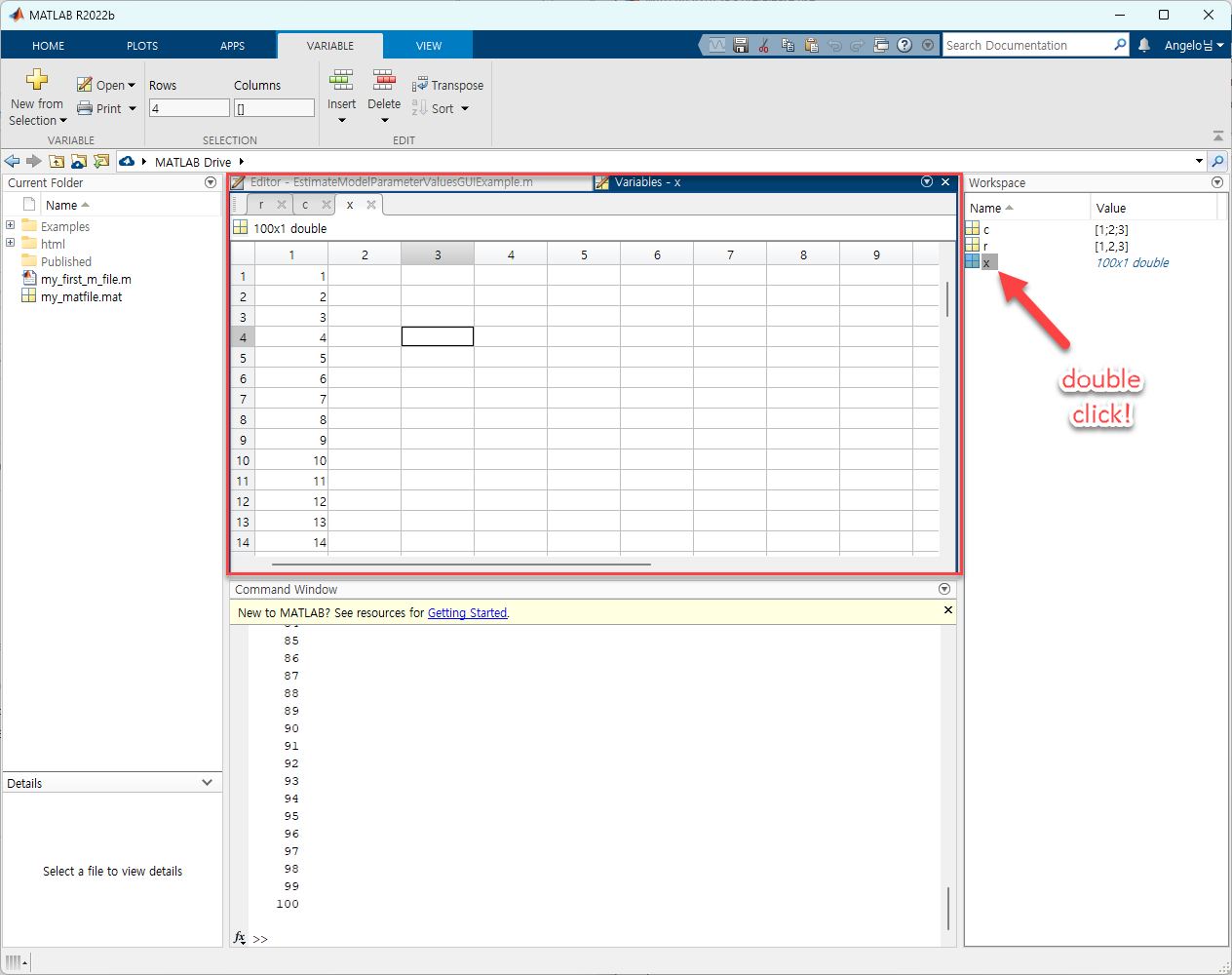
여기서 처음 1은 시작하는 숫자, 가운데 1은 숫자들 사이의 간격, 마지막 100은 벡터의 마지막 숫자이다. Workspace를 확인해보면 x라는 길이 100짜리의 행벡터가 만들어진 것을 확인할 수 있다.

이 방법을 응용해서 100부터 1까지 1씩 줄어드는 길이 100짜리 행벡터를 만들어볼 수도 있다.

y = 100:-1:1

참고로, 이와 같은 방법을 이용해 길이 100짜리 열벡터를 만들고 싶다면 전치 연산을 이용하면 된다. 전치 연산을 수행하는 방법은 아래와 같이 Transpose 버튼을 누르거나, Command Window에서 단따옴표(‘)를 이용하면 된다.

x = x'

또 다른 등간격 벡터 만드는 방법으로는 “linspace” 함수를 쓰는 방법이 있다. 이 방법은 등간격 벡터의 “간격” 보다 “벡터 원소의 총 갯수”가 몇 개인지가 더 중요한 경우 사용한다. 가령, 0 부터 10까지 총 4개의 등간격 벡터를 생성하고 싶다면 아래와 같이 입력할 수 있다.

x = linspace(0, 10, 4)

x =

         0    3.3333    6.6667   10.0000

벡터 원소 조작하기

벡터의 원소 꺼내보기

생성한 벡터, 행렬의 원소값들을 꺼내보기 위해선 소괄호(“( )”)를 이용한다. MATLAB에서 특징적인 부분 중 하나는 벡터와 행렬의 인덱스는 0이 아니라 1부터 시작한다는 점이다. 아래의 예시를 확인해보자.

x = [3, 5, 2, 4];
x(1)

ans =

     3

벡터 x 뒤에 소괄호를 이용해 꺼내고자 하는 인덱스 번호 (여기선 1)을 넣으면 첫 번째 원소값인 3이 출력되는 것을 알 수 있다. 만약, 첫번째부터 세 번째까지의 원소를 한번에 얻고 싶다면 다음과 같이 입력할 수 있다.

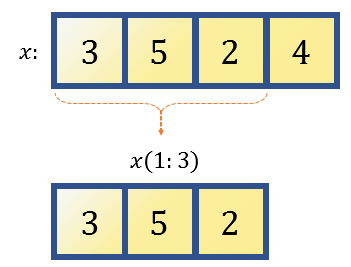
x(1:3)

ans =

     3     5     2

또 만약, 첫 번재 값과 네 번째 원소만 얻고 싶은 경우에는 다음과 같이 벡터를 이용해 indexing을 할 수 있다.

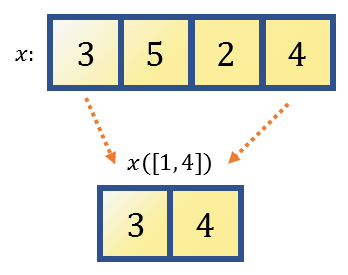
x([1, 4])

ans =

     3     4

또 하나 MATLAB에서 유용하게 쓸 수 있는 indexing 방법은 “end”를 쓰는 것이다. 말 그대로 “end”는 마지막 원소까지를 의미한다.

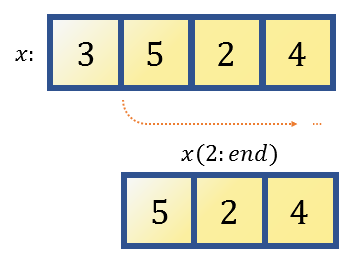
x = [3, 5, 2, 4];
x(2:end)

ans =

     5     2     4

벡터의 원소 제거하기

아래와 같이 벡터의 특정 인덱스 원소를 “[]”로 대체하여 벡터의 원소를 제거할 수 있다. 참고로 “[]”와 같이만 입력하면 아무것도 들어있지 않는 벡터를 의미하므로 벡터의 원소를 “대체한다”고 볼 수 있는 것이다.

x = [3, 5, 2, 4];
x(3) = []

x =

     3     5     4

위의 “원소 꺼내기”에서 여러개의 원소를 한번에 선택할 수 있는 것 처럼 원소 삭제할 때에도 마찬가지로 여러개의 원소를 한번에 삭제할 수 있다.

x = [3, 5, 2, 4];
x(1:2) = []

x =

     2     4

x = [3, 5, 2, 4];
x([1, 4]) = []

x =

     5     2

벡터 합치기(concatenation)

벡터를 합칠 때는 벡터를 정의할 때 처럼 대괄호(“[ ]”)를 이용해 합칠 수 있다.

가령 아래와 같이 두 행벡터를 합칠 수 있다.

x = [1, 2, 3]; y = [4, 5, 6];

new_vec1 = [x, y]
new_vec2 = [x; y]

new_vec1 =

     1     2     3     4     5     6

new_vec2 =

     1     2     3
     4     5     6

아래와 같이 열벡터도 합칠 수 있다. 다만, 어떤 방향으로 합칠지는 사용자가 필요에 따라 결정하면 된다.

x = [1; 2; 3]; y = [4; 5; 6];
new_col1 = [x; y]
new_col2 = [x, y]

다만, 벡터를 합칠 때는 벡터의 크기가 잘 맞는지 확인하는 작업은 꼭 필요하다. 가령 아래와 같이 길이가 다른 두 개의 열벡터를 가로로 합치는 것은 불가능하며 합치고자 하는 벡터들의 차원(dimension)이 맞지 않다는 에러가 출력된다.

x = [1; 2; 3]; y = [4; 5];
new_col3 = [x, y]

Error using horzcat
Dimensions of arrays being concatenated are not consistent.

원소별 연산

원소별 연산은 두 벡터 혹은 행렬 간 대응되는 원소들끼리 수행하는 연산을 의미하며, 원소별 연산을 취하기 위해선 연산자 앞에 점(“.”)을 찍어서 표시한다.

원소별 곱셈은 일반적인 행렬 곱셈과 다르게 말 그대로 원소별로 연산을 하는 경우에 사용한다. 아래의 예시를 보자.

a = [1, 2, 3];
b = [3, 2, 1];

a .* b

ans =

     3     4     3

다시 말해, 원소별 곱셈은 말 그대로 각 원소별로 곱셈이 수행된다. 아래의 그림을 보면 더 잘 이해할 수 있을 것이라 생각한다.

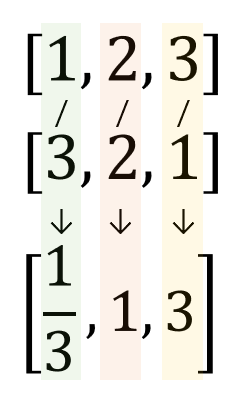
마찬가지로 원소별 나눗셈도 가능하다.

a = [1, 2, 3];
b = [3, 2, 1];

a ./ b

ans =

    0.3333    1.0000    3.0000

또, 원소별 거듭제곱도 가능하다.

a = [1, 2, 3];
b = [2, 2, 2];

a .^ b

ans =

     1     4     9

이 페이지에서 말하는 벡터는 “화살표”로 표현되는 유클리드 벡터가 아닌 “숫자의 나열”로 생각할 수 있는 더 근본적인 의미의 벡터에 가깝다. 이와 관련한 수학적 관점의 논의가 궁금한 사람은 여기에서 확인할 수 있다. ↩

벡터 다루기